Range polynomial climbing hill

Previously, I wrote about SparkEV range by finding a polynomial that fits observed power at various speeds. If you haven't, you should read that first as this post will expand on that idea to cover driving on hills.

http://sparkev.blogspot.com/2016/03/range-polynomial.html

Of course, that post was based on actual measurements and using parameters that mimic physical characteristics of the car, which was covered in an even earlier blog post.

http://sparkev.blogspot.com/2016/01/sparkev-range.html

In this post, we'll discuss what happens to power and range as the car is driven over various hills. Only uphill case will be discussed, because it's more important to know how far one can get up a hill. You can guesstimate that downhill will be 1/2 to 3/4 regeneration back into the battery. As such, starting with full battery charge on top of a hill is not a good idea. One would waste energy by using the friction brakes to slow down rather than getting "free" energy, which also wastes money by wearing out the brakes.

Caveat: these are made up numbers, and should not be trusted!

But remember, these are "made up" numbers, and plenty of seasoning should be used before digesting. See my methodology later in this post and make up your own mind as to the validity.

While the simple case of power on flat road was probably closer to reality, additional power with hill climbing could be way off if the electrical efficiency does not stay constant. For smaller hills where the extra power is not all that much, it's probably accurate enough. But for very steep hills that require almost full power, they will be way off.

How much off? Consider a hill so steep that the car cannot accelerate. Then full 100kW of power out of the battery would be used to maintain whatever speed it had when the hill was first encountered. If that speed was 1 MPH, then the range would be

1 MPH * 18 kWh / 100 kW = 0.18 miles

Worse, let's say the hill was so steep that the car started moving backwards even under full power out of the battery. Then the range would be negative!

However, it's reasonable to assume things are not so bad when the power is much less than 100kW. You might think that efficiency change linearly with power, but that isn't the case. Efficiency explanation is too messy, involving back EMF and such, but you're welcome to research the topic.

How much worse can it be? Without having motor efficiency figures and tables, it's impossible to know. I guesstimate up to about half of full power could be estimated as reasonably close to typical efficiency. So that's a spiciest seasoning: all these figures are probably good enough up to about half the full power. Where did half of full power being "good enough" come from? As I often tell you, 

I JUST MAKE STUFF UP!

Parameters

First is to recognize what the hills are. Typically, hills are specified as percent grade: distance rise over distance run. One can look it up in Wikipedia and other sources to see what they mean.

But what are the typical values? Infinite would be vertical, which is not possible while 100% would be 45 degrees. From google, we find "The National Road (built in 1806) had a maximum grade of 8.75%. Local roads are much higher (12% or 15% are sometimes allowed) Otter Tail MN County roads 6%, alleys 8% Driveways can be as much as 30% for a short distance."

The dreaded "grapevine" (aka Tejon Pass) in CA is under 7% grade for about 12 miles.

http://www.crashforensics.com/tejonpass.cfm

There are steeper roads as well, as steep as 38%. But those roads are far shorter.

http://www.foxnews.com/travel/2014/03/03/worlds-steepest-roads/

For those who are allergic to foxnews, huffpo shows similar.

http://www.huffingtonpost.com/2014/02/28/steepest-streets-america_n_4871559.html

There are also slight slopes in local freeways. I pick following grades and show the corresponding angles and additional force required from the motor.

grade%	0	1	2	3	5	8	13	21	34
degrees	0.0	0.6	1.1	1.7	2.9	4.6	7.4	11.9	18.8
2014 (lb)	0	31	62	93	156	248	402	640	1003
2015/16 (lb)	0	30	60	90	151	241	389	620	971

Keen observers will note that grade numbers are roughly Fibonacci numbers. Yeah, well, we're off by 1.

Angles are simple arc tangent of grades. 2015 weighs 2866 lb and 2014 is heavier at 2967 lb. SparkEV cannot drive itself (yet), so I add 150 lb as driver weight and multiply by the sine of the angle for added force. See theory section below for math explanation.

Something to note is that one could theoretically "push" SparkEV up Tejon pass at 8% grade if they can push 250 lb. I used to be able to do so, but not anymore. This is where having girlfriends with strong muscles could come in handy.

Power

Going up the hill requires extra power (duh!). How much extra depends on weight and speed. Weight is assumed to be empty car's weight + 150 lb (driver). We'll explore heavier case later in this post. Following are plots for additional power required at various speeds and grades.

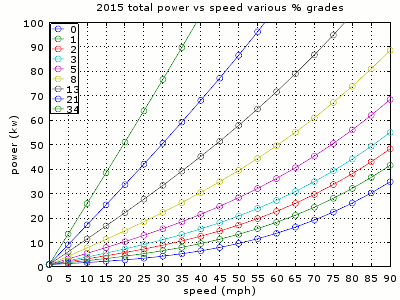
Note that additional power increase linearly with speed. But that doesn't mean going 0% grade will not use power. What's needed is the total power that includes driving at flat road found in previous blog post. Following plots show the total power.

Something of interest would be to estimate the road grade based on car's power. For example, if the car shows power as 30 kW while traveling 45 MPH constant speed, the road has roughly 8% grade (tan color plot). Of course, this is with only the 150 lb driver and making sure there is no acceleration involved; cruise control is helpful. More cargo or twitch on the accelerator pedal will mean less grade, but it is useful as an estimate for maximum grade of  the road.

How well does grade estimation based on power work? For a particular stretch of road that I got 51.1 mi/kWh going down hill, the steep section is about 2.5 miles. From plugshare terrain view, topo map shows the elevation is from 800 ft to 1600 ft, or 800 / 5280 = 0.15 miles. Then the actual grade is

0.15 / ((2.5^2-0.15^2)^0.5) * 100 = about 6%

Driving through this area up hill, power shows between 28 kW to 33 kW at 55 MPH. From the graph, that occurs between 5% grade (magenta color plot) and 8% (tan color plot). That's pretty close, and I'm fairly confident that powers are pretty close to actual, especially at lower power levels under 50 kW. I had the dogs with me that added 125 lb extra. But I'll show later that the extra weight does not change this much at this grade.


Range

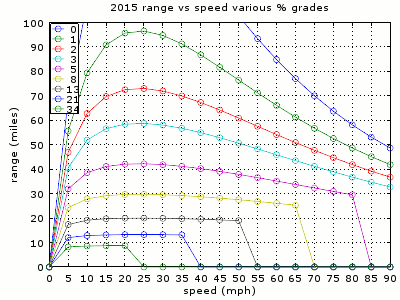
Now we can use total power to estimate the range at various speeds. Following plots show the range vs speeds. SparkEV is capable of 100 kW, but DCFC is only 50 kW, and even 90 MPH on flat road is less than 50 kW. It's not known what may happen when using power greater than 50 kW for extended periods of time, so the grade + speed that result in greater than 50 kW are shown as 0 miles range. One could go faster, but what I show is safest speed based on extended usage (ie, 20 minutes of DCFC).

Unlike the case of constant power use, such as using the heater / AC, that resulted in better range with slight speed increase, the shape of the range over speed for hilly road is the same as flat road case. Therefore, keep the speed low to maximize range, just like how one would drive on flat road for maximum range.

Because the power needed to climb the hill can be substantial, it doesn't extend the range all that much with speed for steeper hills. For example, 8% grade (about that of maximum on Tejon pass) would result in roughly 30 miles range at 25 MPH vs 25 miles range at 65 MPH. As a percentage, it's large, but 5 miles make little difference. If the destination is at the top of a hill, speed is largely irrelevant at grades more than 5%.

However, if one expects to drive beyond the hill top (going down or flat after climb), it may make sense to slow down a bit to save some energy.

Energy

But range isn't as useful. We don't typically drive uphill for entire battery capacity. What we'd like to know is how much energy is used to drive certain number of miles uphill. This would require 3D plot. Simpler is to take some boundary conditions: 25 MPH, 45 MPH, 65 MPH.

Following plots show the energy use over distance for various speeds. Since we're talking about shorter distances, we don't have to play safe with power, and we consider full power case. Power greater than 100kW are shown as full battery energy (not recommended / possible). But remember what I wrote in caveat above: they could be way off with higher power.

25 MPH case

45 MPH case

65 MPH case

Note that SparkEV cannot drive 34% grade at more than 45 MPH. It's just as well; those roads are local, and one should not speed on them.

GVWR case

All of the above are with 150 lb driver, probably the best case. With more passengers and cargo, weight will be more. The maximum weight is the gross vehicle weight rating. I can't seem to find this number through google, but I find it printed on the car's door as 3761 lb (3761-2866 = 895 lb of "cargo"). Only 2015 data is available.

But there is a problem. With added weight, there will be more friction from rolling from the tires and wheel bearings. Since the range polynomial was derived using "light weight" as cargo, it could be very different with full GVWR. Unfortunately, we can't do much about that since we don't have the data; we can only assume things will be worse. Did I mention I make stuff up?

Then we have the following. Remember, actual will be worse, though not quantified how much worse. And again, remember the caveat about higher power efficiency being much different than typical.

Something to note is that top speed at GVWR is only 40 MPH on 34% grade hills. It's just as well; on such steep hill, even 25 MPH might seem scary.

Recall from total power discussion above that I drove 55 MPH through 6% grade and the power display showed between 28 kW and 33 kW with two dogs, about 125 lb extra. Even if I had almost 750 lb extra, the power would be only slightly more, maybe around 35 kW. Of course, this still neglects the rolling resistance effect, but it should be pretty close.

Can SparkEV climb Tejon Pass?

In theory, SparkEV can easily climb over Tejon Pass. It's only 6% grade for about 12 miles.

First, let's check the power. 8% grade at 65 MPH is about 50kW (half power) while 5% grade is much less. 6% grade at 65 MPH would probably (PROBABLY) have similar efficiency as typical, so we can use above plots.

On the way down, it would recapture 50% to 75% of the energy via regenerative braking. But the problem is how much energy would it have when it gets to the bottom of the hill before the actual climb. If there's DCFC at the bottom of the hill, this is not a problem. Alas, that isn't the case.

Going from South to North as of Mar. 2016, closest DCFC is at Castaic (1200 ft), some 36 miles away from Gorman peak at about 4200 ft, difference of 3000 ft (0.57 miles).

23901 Creekside Rd, Santa Clarita, CA 91355

That is average of 0.57 / 36 = 1.6% grade. Let's assume 2% (red color plot from 65 MPH energy graph) and things operate within the model parameters (efficiency stays at typical levels).

2015 SparkEV would easily make it at 65 MPH for 35 miles of 2% grade with solo driver by using 70% to 80% of new battery capacity. Given that battery warranty kicks in at 65%, one could theoretically make it over the hill even with slightly worn battery. Remember, we need some margin, so we don't consider 100% case. Another interesting data is that average power required is roughly that of driving at 80 MPH on flat road.

For GVWR case, it's unknown, because the range polynomial doesn't take added rolling resistance into account. But we can guesstimate by taking 3% grade case (about double actual grade, cyan color plot). That shows 65 MPH for 35 miles to use over 90% of new battery capacity. Unless one has a new battery and charged to 100%, SparkEV isn't likely to make it over the hill. It's also about average power at 90 MPH on flat road.

But what if we go really slowly? It's too dangerous to drive at 25 MPH on freeway, so one should not do this. But as a thought experiment, is it possible? From 25 MPH graph, we see that 3% grade for 35 miles will need about 70% to 80% battery. So in theory, one can make it over the hill going really slowly. It's also about average power at 50 MPH on flat road, but going half the speed.

Going up to the top of the hill is one thing, but getting to the charger on the other side is equally important. Next DCFC is located at Selma, CA, some 180 miles away from previous DCFC at Castaic.

2950 Pea Soup Anderson Blvd, Selma, CA 93662

This would make it impossible to use DCFC to travel over Tejon Pass. There really need to be DCFC at the bottom of the hill on both sides for this to work. For now, the only option for SparkEV is along 101 freeway to travel between SoCal and NoCal as in my fictional trans CA EV race blog post.

http://sparkev.blogspot.com/2016/02/the-great-trans-california-ev-race.html

Theory

Theory on the basics of range polynomial was discussed in previous blog post, aptly named "range polynomial". Here, we add additional, which is basic Trigonometry and Physics.

http://i.stack.imgur.com/06flR.gif

In the picture above, W is the weight of the car + cargo. Theta is the angle. But the angle is not given, only percent grade.

Percent grade on a hill is rise over run. Then the angle is simply the arc tangent of percent (divided by 100). A quick review of Trigonometric magic word, so-caaaa-toe-ahhhh.

SOH : Sine of an angle is Opposite side length divided by Hypotenuse length of a right triangle.
CAH : Cosine of an angle is Adjacent side length divided by Hypotenuse length of a right triangle.
TOA : Tangent of an angle is Opposite side length divided by Adjacent side length of a right triangle.

Quick side note: sine in Spanish is "seno" which is also the body part. Math and anatomy, like peas in a pod!

We invoke the TOA clause from above, and take inverse tangent (aka, arc tangent) to get the angle.

Angle = arctan (grade_in_percent / 100)

Once we have the angle, we can simply multiply the weight by the sine of the angle to find the additional force needed. Of course, we don't really need that at all; we can use Pythagorean theorem to bypass sine and tangent altogether, but that's left as exercise to your high school kids taking Trigonometry.

Once the force is known, we need to find the power needed to overcome the added force as the car is traveling up. Obviously, faster speed, quicker one would acquire potential energy. It's simply force multiplied by speed.

power_climbing = force * speed

Because the power is specified as kiloWatts, conversions are needed. Doing bunch of hocus pocus conversions from magic miles and pound and slugs to MKS units, we arrive at power just for the climbing portion in kiloWatts.

Because the operations are linear, power will simply add. You can prove it yourself or pay your kids to do it. We add flat road power from range polynomial to the additional power for climbing to get the total power for climbing at various speeds.

power_total = power_flat_road + power_climbing

Once we have the total power, we can multiply by time needed to travel some distance to find the required energy. Time, of course, is distance divided by speed. Once again, make sure the units are converted to MKS and arrive at the following.

Energy = power_total * time = power_total * (distance / speed)

After all this, we generate various plots of interest. Are they correct? It's homework!

Edit Apr. 5, 2016

After some discussion on unrelated topic of SparkEV's fake noise maker (thanks for poking me, Norton), aka Pedestrian Friendly Alert Feature, PFAF (completely useless as my Prius is silent), I thought of a new way to estimate rolling resistance. It is roughly when low speed has about 1/2 of the range of flat road. From above, that occurs at about 2% grade (65 miles at 10 MPH). That shows the force to be about 60 lb.

While air resistance may not be substantial at 10 MPH, static power of 1 kW could be taking significant portion. Plugging in the number to polynomial, 10 MPH result in 1.66kW, taking 60%. Then the rolling resistance force is 40% of 60 lb, or 24 lb.

One can experiment this value on flat road. Using a bathroom scale pressed against the back of the bumper, push the car until it's moving at constant speed. I read about 35 lb when I do this, though it's changing much due to irregular pushing. I think that's close enough, so it's about 35/3100 = 1.13%

Then the force calculation in appendix should change as follows. Since baseline includes the weight of the car and 150 lb driver, added force is only applicable to added weight minus the baseline.

  if (year==2014) mass_baseline = (2967+150); end
  if (year==2015) mass_baseline = (2866+150); end
  force1 = ( mass_lb  * sin(angle_radians) ...
           + ( mass_lb - mass_baseline)  * 0.0113 * cos(angle_radians) ...
           ) / 2.2 * gravity; % Newtons

Below are new graphs for GVWR case for 2015. Range penalty is about 5 miles for low slopes with GVWR.

Appendix

As before, Octave is used to analyze and generate the plots. New convention is adopted for this m-file: those ending with "1" are vectors (1D arrays) and "2" are matrices (2D arrays). For example, "force1" would indicate 1D array of force values.

Copy-paste this into Octave to generate the plots or save to a file and play with it as you see fit. What grade would SparkEV fail to climb at any speed? What road would SparkEV fail to travel at specified speed limit due to steep grade?

clear; close all;

batt_2014 = 19;
speed1_2014=[0 24 55 62];
power1_2014=[1 3.33 10.2 12.7];

batt_2015 = 18;
speed1_2015=[0 30 55 60];
power1_2015=[1 3.9 10.6 12.73];

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% power polynomial and max range

poly1_2014=polyfit(speed1_2014, power1_2014, 3)
poly1_2015=polyfit(speed1_2015, power1_2015, 3)

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% range over slope

function added_power_vs_speed(year, mass_lb, poly1, batt)
  speed1=0:5:90;
  grade1=[0 1 2 3 5 8 13 21 34]; %grade in percent
  mph2kmps = 0.44704 / 1000;
  gravity = 9.8; %m/sec/sec
  angle_radians=atan(grade1/100); %radians

  % OLD! force1 = mass_lb / 2.2 * gravity * sin(angle_radians); % Newtons
  if (year==2014) mass_baseline = (2967+150); end
  if (year==2015) mass_baseline = (2866+150); end
  force1 = ( mass_lb  * sin(angle_radians) ...
           + ( mass_lb - mass_baseline)  * 0.0113 * cos(angle_radians) ...
           ) / 2.2 * gravity; % Newtons

  % power only to overcome hill
  force2 = repmat(force1, length(speed1), 1)';
  speed2 = repmat(speed1, length(force1), 1);
  power_grade2 = force2 .* speed2 * mph2kmps; % kW extra for grades

  figure; plot(speed1, power_grade2, 'o-'); grid on;
  axis([min(speed1) max(speed1) 0 100]);
  set(gca, 'xtick', speed1, 'ytick', 0:10:100);
  xlabel('speed (mph)'); ylabel('power (kw)');
  legend(cellstr(num2str(grade1')),  "location", "northwest");
  title ([num2str(year) ' extra power vs speed various % grades']);

  % total power including extra power for grades
  power1 = polyval(poly1, speed1);
  power2 = repmat(power1, length(force1), 1) + power_grade2;

  figure; plot(speed1, power2, 'o-'); grid on;
  axis([min(speed1) max(speed1) 0 100]);
  set(gca, 'xtick', speed1, 'ytick', 0:10:100);
  xlabel('speed (mph)'); ylabel('power (kw)');
  legend(cellstr(num2str(grade1')),  "location", "northwest");
  title ([num2str(year) ' total power vs speed various % grades']);

  % ranges at slopes
  range2 = speed2 * batt ./ power2;
  range2(power2>50) = 0;
  figure; plot(speed1, range2, 'o-'); grid on;
  axis([min(speed1) max(speed1) 0 100]);
  set(gca, 'xtick', speed1, 'ytick', 0:10:100);
  xlabel('speed (mph)'); ylabel('range (miles)');
  legend(cellstr(num2str(grade1')),  "location", "northwest");
  title ([num2str(year) ' range vs speed various % grades']);

  %energy use over distance
  miles2meters = 1/1609.344;
  hour2seconds = 3600;
  distance1 = 0:5:50;
  for speed_a1 = 25:20:65
    force2 = repmat(force1, length(distance1), 1)';
    power_grade2 = force2 * speed_a1 * mph2kmps; % kW extra for grades
    power2 = polyval(poly1, speed_a1) + power_grade2;

    distance2 = repmat(distance1, length(force1), 1); %miles
    time2 = distance2 ./ speed_a1; %hours
    energy2 = power2 .* time2;
    energy2(power2 > 100)=batt;

    figure; plot(distance1, energy2, 'o-'); grid on;
    axis([min(distance1) max(distance1) 0 batt]);
    set(gca, 'xtick', distance1, 'ytick', round((0:(batt/10):batt)*10)/10);
    xlabel('distance (miles)'); ylabel('energy (kWh)');
    legend(cellstr(num2str(grade1')),  "location", "northwest");
    title ([num2str(year) ' energy vs distance at ' ...
            num2str(speed_a1) 'mph various % grades']);
  end

endfunction

added_power_vs_speed(2014, 2967+150, poly1_2014, batt_2014);
added_power_vs_speed(2015, 2866+150, poly1_2015, batt_2015);
added_power_vs_speed(2015, 3761, poly1_2015, batt_2015); %GVWR, 900 lb of cargo

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%resize all plots for easy viewing

% for n=1:18; a=figure(n); set(a, 'Position',[200,100,440,300]); end

Range polynomial

Previously, I wrote a blog post in trying to analyze SparkEV's range. It was done using known parameters of the car, such as weight, drag coefficient, and some guesses as to rolling resistance and efficiency. Basically, it was an attempt to model the car and estimate the range. If you haven't already, that blog post should be read first, because I discuss where the real world data comes from.

http://sparkev.blogspot.com/2016/01/sparkev-range.html

Since we're guessing some parameters, we can ignore the entire car, and only use observed range data to make some models. In this blog post, we'll do just that: model the power using polynomial, and derive the range and other interesting values using the polynomial. In short,

WE'LL JUST MAKE STUFF UP!

As such, one should read this blog post with plenty of seasoning (ie, should not trust any of it). I'll describe my methodology later in this post, so you can judge for yourself how accurate they might be.

Below are plots of ranges as functions of speeds and various battery capacities.

Because the graphs show maximum ranges at various speeds and various battery capacities, one can estimate the range for partial battery. For example, if one charges 14 kWh using DCFC, and speed is about 45 MPH with little stopping, the maximum range for each DCFC session would be about 85 miles. If one charges 1.5 hours using 3.3kW L2AC (assume 80% efficient = 4kW) and drove at 45 MPH, maximum could be about 25 miles. As always, leave 10 miles as margin, so the actual could be 75 miles and 15 miles, respectively. Again, this is without running down the battery completely, but merely to get back to state of charge before the drive began.

One can also guesstimate the battery capacity. For example, if one normally got 75 miles with 10 miles remaining driving 60 MPH with new battery that would be 18 kWh battery. Later, if he (or she; hi Lindsay!) is getting 60 miles with 10 miles remaining under same conditions (same road, driving habit, weather, etc), then the battery capacity would be about 15 kWh.

Range with extra power use

Another interesting graph is to find what happens when extra power is used, such as with heater, AC, open windows with dogs sticking their heads out. The plots show ranges at speeds for various additional power use in kW. They are based on brand new battery, so old battery ranges would not apply. Still, one can get a "feel" for what extra power use would do to the range.

To read the graph, you have to convert the parameters to power in kW. For example, we can assume the heater takes 2kW on average, about two space heaters you might have in the bathroom, and windows up and driving at constant speed at 65 MPH. Then the maximum range would be bit under 70 miles with 2015 (red line). Leaving 10 miles as margin, usable range would be 60 miles.

But if you decided to waste energy by rolling down the windows and blasting the heater, that could result in lot more power use. Let's guess 9 kW. Then the range at 65 MPH for 2015 would be bit under 50 miles (also red line), with 10 miles as margin would leave about 40 miles.

We really should investigate lower battery capacity range with additional power use. I could do that and generate a 3 dimensional plot, but there'd be no way to effectively display it without using some active code such as Javascript. I hate active code in a web page; it's just inviting malware. Ah, the good old days of strict HTML when you never had to worry about malware, but I digress.

What we can do is to find the worst case battery degradation, and use that as the basis for additional power drain. What is the worst case? SparkEV battery warranty is to about 65% capacity (35% below peak). According to MrDRMorgan of forum, this is found in warranty booklet page 14.

http://www.mychevysparkev.com/forum/viewtopic.php?f=9&t=4457&start=28

Then I guesstimate 60% capacity as maximum degradation, and plot the ranges with additional power drains.

For 2015 with worst degraded battery driven at 65 MPH and 4 kW for heater use would result in about 35 miles range. With 10 miles of margin, usable would be 25 miles range. Of course, you can turn off the heater, radio, lights, and windows up in order to result in 45 miles (35 miles with margin). Yup, that's pretty bad, but it'd still be usable if one commutes only 40 miles a day (20 miles each way).

If one can charge at work, even using the heater would be fine or 40 miles each way. And if the commute happen to be only on local road or in Los Angeles (entire city is one giant traffic mess), the range could still be be close to 80 miles (40 miles each way, or 80 miles one way with charging at work). But 80 miles in LA could take 4 hours; what, you get to work and clock out right away?

miles per kWh with extra power use

Sometimes, forum discussion turns to miles per kWh battery used (hi Norton). We know someone did 7.2 mi/kWh for entire battery capacity using 2014 model (see previous blog post on range). But what would it be for various speeds and extra power use, such as heater? If one drives at local speeds (35 MPH), he'd get far higher mi/kWh than driven at freeway speeds (65 MPH). Below graphs show just that.

Without any extra energy use (no heater, AC), one can expect pretty high mi/kWh at low speeds in local roads and traffic. Regenerative braking won't be 100% efficient, so it would take away from this with lots of braking. Still, careful driving could result in close to 8 mi/kWh (or 270 MPGe energy strictly from battery to wheels)

Because these are only dependent on car's geometry, and not battery capacity, these numbers hold regardless of battery capacity. That assumes battery efficiency would not change as it degrades, which is not correct. Still, the battery should not be as big a factor compared to other parameters. Did I mention that I make stuff up?

How they're made

There's a saying, if you want to eat sausage, don't find out how they're made. In this case, you probably want to find out how the plots are made. I mean, you drive a SparkEV, presumably because you did the research to find that it's the best car in the world, and not just as EV. Put it another way, you have to be smart and inquisitive to be a SparkEV driver. I think that's probably why Chevy has been limiting SparkEV sales: not enough smart people in the world. :-)  (Unfortunately in my case, I happened on it by coincidence, not due to any smart research)

Anyway, let's get to it. What we need is power at various speeds and battery capacity. Once they are known, we can find out everything else (range, mi/kWh, etc) without knowing anything about the car, or whether it's a car or a potato.

Once we have the data, we can find a function that fits the data. As you might recall from basic Calculus, polynomials with enough order can fit just about everything. If there's infinite data, we can use infinite order polynomial series (prove it, Mr. Taylor!). Even without infinite data, we can use the polynomial to make up infinite data using the function to find data we don't actually have, and it should be pretty close to actual.

Polynomial theory

So the secret sauce is the combination of sparse, but enough data (not infinite) for power use over speed, and some polynomial function that fits the data. But there's a problem. We don't have a lot of data. As such, that will limit the polynomial order. But we also know that car's aerodynamic power is cube of speed. Then the minimum polynomial should be third power with some coefficients as follows.

(coeff1 * speed^3) + (coeff2 * speed^2) + (coeff3 * speed) + coeff4 = power

For third order polynomial, we need at least 4 data points of speed and corresponding power. Unfortunately, there aren't many. One is by bicycleguy at 0 MPH (1.25 kW). I have "rough" power at 30 MPH=3 to 4 kW and 60 MPH=12 to 13 kW. We have to extract power from other measurements. Following are available.

2014 model = 140 miles at 24 MPH at 7.2 mi/kWh (digital trends)
2014 model = 98 miles at 62 MPH at 5 mi/kWh (Tony Williams)
2015 model = 93 miles at 55 MPH at 5.166 mi/kWh (me! 93/18kWh=5.166 mi/kWh)

Converting to power is speed divided by mi/kWh. Then we have the following.

2014: 0=1.25kW, 24=3.33kW, 62=12.4kW
2015: 0=1.25kW, 30=3 to 4 kW, 55=10.6kW, 60=12 to 13kW

Oops, 2014 is only 3 data while 2015 has range of power for speed at 30 MPH and 60 MPH. Due to lack of display resolution, 2015 power figure accuracy suffer far more. This is where hocus pocus make up stuff as you go along come into play. It's pure fantasy mixed in with some reality.

We know that everything should result in higher power use. That means all the coefficients of the polynomial must be positive numbers. Yes, there could be some higher order effects (100th order?) that could cause our tiny 3rd order polynomial to exhibit weird behavior, but by and large, we can just guesstimate those effects to be small. Did I mention we make stuff up as we go along?

Making stuff up

First, let's assume 1 kW at 0 MPH rather than 1.24 kW. It could be that bicycleguy had the lights on and his radio playing when he measured it. Besides, 1 is lot quicker to type than 1.24.

2015 data is lot more tricky, because the display did not have enough resolution. In-between could be anything. Two data we have that are "pretty close" are 0 and 55 MPH. We can guesstimate 30 MPH as something like 3.5 kW and 60 MPH to be something like 12.5 kW to start.

We plug in 2015 data to Octave (or Matlab) polynomial estimator, we get some values. Then some coefficients are negative! Especially troubling is the third order coefficient being negative. That means SparkEV would eventually generate power when going fast enough. There's no new Physics here, simple error in value. Then we play with the values (leaving 0 MPH at 1 kW) by tweaking small amounts until we have all positive coefficients.

2015: 0=1kW, 30=3.9kW, 55=10.6kW, 60=12.73kW

We have to come up with one additional data point for 2014 model. Given that 2014 is taller gear (motor spins lower RPM), we can guesstimate 55 MPH power could be slightly less than 2015. How much less? I don't know, let's just start with 10.5 kW. Then we do hocus pocus with the polynomial estimator and values until we get all positive coefficient. The result I like happens at the following.

2014: 0=1kW, 24=3.33kW, 55=10.2kW, 62=12.7kW

Something you should be aware is that the coefficients are extremely sensitive to data. If you'd like, you can do the sensitivity analysis, but since the data are "made up" anyway, analysis won't mean much. For now, we have all positive coefficients, making it consistent with the laws of Physics in our third order polynomial universe. Then the coefficients are as follows:

2014: 2.1007e-005, 6.0466e-004, 7.0472e-002, 1
2015: 3.5859e-005, 6.7172e-005, 6.2379e-002, 1

What's interesting is that the linear term for  2015 is less than 2014. Since the linear term is related to weight, and 2015 weighs less than 2014, this is consistent with that. But then the gearing is different, too, so one could say that's also bogus rationale. The life of meta analysis is full of make beliefs.

Polynomial made up data

Using the polynomial, we can plot power and range over speeds. The equation for range is simply speed / power * battery where battery is 19 kWh for 2014 and 18 kWh for 2015.

Note that the ranges for 2014 at 24 MPH and 62 MPH are pretty close to the actual values found through experiment. For 2015, only range data I have is 55 MPH, which is also close to the actual; 62 MPH is also close to what was found by TonyWilliams. However, all of them are slightly lower than experimental data (ie, these are conservative values).

1000 miles a day revisited

Now that we have more uniform data, we can revisit our 1000 miles a day test. The data may not be accurate, but they are at least uniform (accuracy? reality? they don't mean jack!) 1000 miles / 24 hours = 41.667 MPH. With 20 minutes of DCFC + 10 minutes to get on/off the freeway, we have to keep an average speed of 41.7 MPH to drive 1000 miles a day. Below is a plot of average speed over driving speed.

Note the red line for 41.7 MPH and another line for 20.8 MPH needed for 500 miles a day.2014 SparkEV with new battery could easily make 1000 miles a day, even when driven at 65 MPH. But with 2015 SparkEV, it could barely make it when driven at 70 MPH or 75 MPH (72.5 MPH?). So far, all the indications are that SparkEV should be able to drive 1000 miles in a day.

You might poo-poo 1000 miles a day as something insignificant, but many cars without DCFC can't even drive 500 miles in a day.

For example, Fiat 500e has 87 miles range, 24 kWh battery, 6.6 kW on-board charger. Let's assume 95 miles range at 65 MPH (1.46 hours) and 22 kWh (22 kWh / 6.6 kW / 85% efficiency = 3.92 hours). Then the average speed is only 95 / (1.46+3.92) = 17.6 MPH. That's not even enough to drive 500 miles in a day. 500e would need 112 miles range with 22 kWh to achieve 500 miles a day (5.1 mi/kWh). Given that 500e is less efficient than SparkEV, and SparkEV can barely reach 4.2 mi/kWh at 65 MPH (see plot way above), it's unlikely 500e could ever reach 500 miles a day.

In another example, 24kWh Nissan Leaf DCFC is far slower than SparkEV. While it's not known how much slower over typical case for different cars and weather, we can guesstimate 20 minutes for 11 kWh (vs 20 min for 13.5 kWh for SparkEV). You can do the math, but that's not nearly enough to get 1000 miles a day; however, it would be enough to clear 500 miles a day. 30 kWh may be able to clear 1000 miles a day; that's left as exercise to Leaf owners who care to experiment.

Edit: 2016-10-20

Someone drove over 1000 km in one day (16 hours) with SparkEV! That might be one day distance record for SparkEV. Below is the video.

Below is the discussion. It's in French since he's in Canada (yes, they sell SparkEV in Canada, Mexico, and Korea), but you can use google translate to view in any language.

http://menu-principal-forums-aveq.1097349.n5.nabble.com/1000km-en-une-journee-td53319.html

It works out to 1050 km (650 miles) in 16 hours, which is 65.6 km/hr (40.6 MPH) on average. Had he driven 24 hours in same pattern, he would've driven 1575 km (975 miles). Such feat would not be possible with slower charging EV like Nissan Leaf (24 kWh version) or EV without DCFC like Fiat 500e.

So for now, the real world range of SparkEV per day is 1050 km (650 miles) while leaving 8 hours for sleeping and extrapolated 1575 km (975 miles) in 24 hours without sleeping.

Conclusion

In this post, I tried to make up data that at least better fit known experimental values, and used lowest order polynomial to estimate various scenarios. Given enough time and money, one could obtain better data and better polynomial that would account for many other aspects of the car. But for now, this simple polynomial should be enough to get a rough idea of SparkEV performance over various battery capacities and energy use, and another hint to a possibility of 1000 miles a day.

Appendix

All plots and analysis were generated using Octave (freeware Matlab clone), but Matlab should work as well. You can get Octave from

https://www.gnu.org/software/octave/download.html

Below is my "m file". Copy-paste into Octave, or you can save it to a file and tweak as you see fit.

clear; close all;

speed=0:5:90;

batt_2014 = 19;
speed_2014=[0 24 55 62]; 
power_2014=[1 3.33 10.2 12.7]; 

batt_2015 = 18;
speed_2015=[0 30 55 60];
power_2015=[1 3.9 10.6 12.73]; 

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% power polynomial and max range

poly_2014=polyfit(speed_2014, power_2014, 3)
power_2014=polyval(poly_2014, speed); 
range_2014=speed./power_2014*batt_2014;

poly_2015=polyfit(speed_2015, power_2015, 3)
power_2015=polyval(poly_2015, speed); 
range_2015=speed./power_2015*batt_2015;

% plot power vs speed
figure;
plot(speed, power_2014, 'o-', speed, power_2015, 'o-');
axis([0 90 0 40]); grid on;
set(gca, 'xtick', speed, 'ytick', 0:5:40);
title('SparkEV power'); xlabel('Speed (mph)'); ylabel('power (kW)');
legend('2014', '2015/16'); 

% plot range vs speed
figure;
plot(speed, range_2014, 'o-', speed, range_2015, 'o-');
axis([0 90 40 150]); grid on; 
set(gca, 'xtick', speed, 'ytick', 40:10:150);
title('SparkEV range'); xlabel('Speed (mph)'); ylabel('range (miles)');
legend('2014', '2015/16'); 

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% function to have uniform range vs speed plot axis

function plot_speed_range(speed, ranges, legend_val)
  plot(speed, ranges, 'o-'); 
  axis([0 90 0 140]); grid on; 
  set(gca, 'xtick', speed, 'ytick', 0:10:140);
  xlabel('Speed (mph)'); ylabel('range (miles)');
  legend(cellstr(num2str(legend_val')));
endfunction

function plot_speed_mikwh(speed, mikwhs, legend_val)
  plot(speed, mikwhs, 'o-'); 
  axis([0 90 0 8]); grid on; 
  set(gca, 'xtick', speed, 'ytick', 0:8);
  xlabel('Speed (mph)'); ylabel('miles/kwh');
  legend(cellstr(num2str(legend_val')));
endfunction

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% ranges for various battery capacity

function range_over_battery(batt, speed, power)
  N=15;
  batt_var = 0:(N-1);
  batts_var = repmat(batt_var, length(power), 1)';
  powers = repmat(power, N, 1);
  ranges = repmat(speed, N, 1) ./ powers .* (batt - batts_var);  
  plot_speed_range(speed, ranges, batt-batt_var);
endfunction

figure;
range_over_battery(batt_2014, speed, power_2014);
title('2014 SparkEV ranges for various battery kWh');

figure;
range_over_battery(batt_2015, speed, power_2015);
title('2015/2016 SparkEV ranges for various battery kWh');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% ranges for various power levels

function range_over_power(batt, speed, power)
  N=10;
  power_var = 0:(N-1);
  powers_var = repmat(power_var, length(power),1)';
  powers = repmat(power, N, 1) + powers_var;
  ranges = repmat(speed, N, 1) ./ powers * batt;  
  plot_speed_range(speed, ranges, power_var);  
endfunction

figure;
range_over_power(batt_2014, speed, power_2014);
title('2014 SparkEV ranges for various power use');
figure;
range_over_power(batt_2015, speed, power_2015);
title('2015/2016 SparkEV ranges for various power use');

figure;
range_over_power(batt_2014*.6, speed, power_2014);
title('2014 SparkEV worst case ranges for various power use');
axis([0 90 0 90]); set(gca, 'ytick', 0:10:90);
figure;
range_over_power(batt_2015*.6, speed, power_2015);
title('2015/2016 SparkEV worst case ranges for various power use');
axis([0 90 0 90]); set(gca, 'ytick', 0:10:90);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% mi/kwh for various power levels

function mikwh_over_power(speed, power)
  N=10;
  power_var = 0:(N-1);
  powers_var = repmat(power_var, length(power),1)';
  powers = repmat(power, N, 1) + powers_var;
  speeds = repmat(speed, N, 1);
  mikwhs = speeds ./ powers;
  plot_speed_mikwh(speed, mikwhs, power_var);
endfunction

figure;
mikwh_over_power(speed, power_2014);
title('2014 SparkEV mi/kWh for various power use');
figure;
mikwh_over_power(speed, power_2015);
title('2015/2016 SparkEV mi/kWh for various power use');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Can you drive 1000 miles in a day using multiple DCFC?

batt1k_2014=13.25;
range1k_2014=speed ./ power_2014 * batt1k_2014;
time1k_2014=batt1k_2014 ./ power_2014; 
speed1k_2014=range1k_2014 ./ (time1k_2014+0.5);

batt1k_2015=batt1k_2014;
range1k_2015=speed ./ power_2015 * batt1k_2015;
time1k_2015=batt1k_2015 ./ power_2015; 
speed1k_2015=range1k_2015 ./ (time1k_2015+0.5);

figure;
plot(speed, speed1k_2014, 'o-'
  , speed, speed1k_2015, 'o-'
  , speed, ones(length(speed), 1)*1000/24, 'r-'
  , speed, ones(length(speed), 1)*500/24, 'm-');
axis([20 90 20 46]); grid on;
set(gca, 'xtick', speed);   set(gca, 'ytick', 20:2:46);
title('SparkEV average speed (20 min for 13.25 kWh + 10 min to get off/on road)'); 
xlabel('Speed while running (mph)'); 
ylabel('Average speed including DCFC time (mph)');
legend(
    '2014 average speed'
  , '2015/2016 average speed'
  , '41.7 mph needed for 1000 miles a day'
  , '20.8 mph needed for 500 miles a day'
  , "location", "southeast");

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%resize all plots for easy viewing

% for n=1:11; a=figure(n); set(a, 'Position',[200,100,440,300]); end