http://sparkev.blogspot.com/2016/03/range-polynomial.html
Of course, that post was based on actual measurements and using parameters that mimic physical characteristics of the car, which was covered in an even earlier blog post.
http://sparkev.blogspot.com/2016/01/sparkev-range.html
In this post, we'll discuss what happens to power and range as the car is driven over various hills. Only uphill case will be discussed, because it's more important to know how far one can get up a hill. You can guesstimate that downhill will be 1/2 to 3/4 regeneration back into the battery. As such, starting with full battery charge on top of a hill is not a good idea. One would waste energy by using the friction brakes to slow down rather than getting "free" energy, which also wastes money by wearing out the brakes.
Caveat: these are made up numbers, and should not be trusted!
But remember, these are "made up" numbers, and plenty of seasoning should be used before digesting. See my methodology later in this post and make up your own mind as to the validity.
While the simple case of power on flat road was probably closer to reality, additional power with hill climbing could be way off if the electrical efficiency does not stay constant. For smaller hills where the extra power is not all that much, it's probably accurate enough. But for very steep hills that require almost full power, they will be way off.
How much off? Consider a hill so steep that the car cannot accelerate. Then full 100kW of power out of the battery would be used to maintain whatever speed it had when the hill was first encountered. If that speed was 1 MPH, then the range would be
1 MPH * 18 kWh / 100 kW = 0.18 miles
Worse, let's say the hill was so steep that the car started moving backwards even under full power out of the battery. Then the range would be negative!
However, it's reasonable to assume things are not so bad when the power is much less than 100kW. You might think that efficiency change linearly with power, but that isn't the case. Efficiency explanation is too messy, involving back EMF and such, but you're welcome to research the topic.
How much worse can it be? Without having motor efficiency figures and tables, it's impossible to know. I guesstimate up to about half of full power could be estimated as reasonably close to typical efficiency. So that's a spiciest seasoning: all these figures are probably good enough up to about half the full power. Where did half of full power being "good enough" come from? As I often tell you,
I JUST MAKE STUFF UP!
Parameters
First is to recognize what the hills are. Typically, hills are specified as percent grade: distance rise over distance run. One can look it up in Wikipedia and other sources to see what they mean.
But what are the typical values? Infinite would be vertical, which is not possible while 100% would be 45 degrees. From google, we find "The National Road (built in 1806) had a maximum grade of 8.75%. Local roads are much higher (12% or 15% are sometimes allowed) Otter Tail MN County roads 6%, alleys 8% Driveways can be as much as 30% for a short distance."
The dreaded "grapevine" (aka Tejon Pass) in CA is under 7% grade for about 12 miles.
http://www.crashforensics.com/tejonpass.cfm
There are steeper roads as well, as steep as 38%. But those roads are far shorter.
http://www.foxnews.com/travel/2014/03/03/worlds-steepest-roads/
For those who are allergic to foxnews, huffpo shows similar.
http://www.huffingtonpost.com/2014/02/28/steepest-streets-america_n_4871559.html
There are also slight slopes in local freeways. I pick following grades and show the corresponding angles and additional force required from the motor.
| grade% | 0 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
| degrees | 0.0 | 0.6 | 1.1 | 1.7 | 2.9 | 4.6 | 7.4 | 11.9 | 18.8 |
| 2014 (lb) | 0 | 31 | 62 | 93 | 156 | 248 | 402 | 640 | 1003 |
| 2015/16 (lb) | 0 | 30 | 60 | 90 | 151 | 241 | 389 | 620 | 971 |
Keen observers will note that grade numbers are roughly Fibonacci numbers. Yeah, well, we're off by 1.
Angles are simple arc tangent of grades. 2015 weighs 2866 lb and 2014 is heavier at 2967 lb. SparkEV cannot drive itself (yet), so I add 150 lb as driver weight and multiply by the sine of the angle for added force. See theory section below for math explanation.
Something to note is that one could theoretically "push" SparkEV up Tejon pass at 8% grade if they can push 250 lb. I used to be able to do so, but not anymore. This is where having girlfriends with strong muscles could come in handy.
Going up the hill requires extra power (duh!). How much extra depends on weight and speed. Weight is assumed to be empty car's weight + 150 lb (driver). We'll explore heavier case later in this post. Following are plots for additional power required at various speeds and grades.
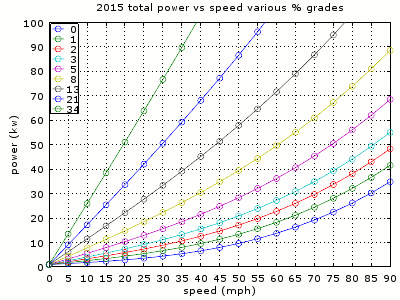
Note that additional power increase linearly with speed. But that doesn't mean going 0% grade will not use power. What's needed is the total power that includes driving at flat road found in previous blog post. Following plots show the total power.
Something of interest would be to estimate the road grade based on car's power. For example, if the car shows power as 30 kW while traveling 45 MPH constant speed, the road has roughly 8% grade (tan color plot). Of course, this is with only the 150 lb driver and making sure there is no acceleration involved; cruise control is helpful. More cargo or twitch on the accelerator pedal will mean less grade, but it is useful as an estimate for maximum grade of the road.
How well does grade estimation based on power work? For a particular stretch of road that I got 51.1 mi/kWh going down hill, the steep section is about 2.5 miles. From plugshare terrain view, topo map shows the elevation is from 800 ft to 1600 ft, or 800 / 5280 = 0.15 miles. Then the actual grade is
0.15 / ((2.5^2-0.15^2)^0.5) * 100 = about 6%
Driving through this area up hill, power shows between 28 kW to 33 kW at 55 MPH. From the graph, that occurs between 5% grade (magenta color plot) and 8% (tan color plot). That's pretty close, and I'm fairly confident that powers are pretty close to actual, especially at lower power levels under 50 kW. I had the dogs with me that added 125 lb extra. But I'll show later that the extra weight does not change this much at this grade.
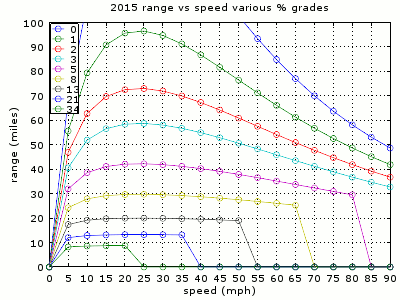
Range
Now we can use total power to estimate the range at various speeds. Following plots show the range vs speeds. SparkEV is capable of 100 kW, but DCFC is only 50 kW, and even 90 MPH on flat road is less than 50 kW. It's not known what may happen when using power greater than 50 kW for extended periods of time, so the grade + speed that result in greater than 50 kW are shown as 0 miles range. One could go faster, but what I show is safest speed based on extended usage (ie, 20 minutes of DCFC).
Unlike the case of constant power use, such as using the heater / AC, that resulted in better range with slight speed increase, the shape of the range over speed for hilly road is the same as flat road case. Therefore, keep the speed low to maximize range, just like how one would drive on flat road for maximum range.
Because the power needed to climb the hill can be substantial, it doesn't extend the range all that much with speed for steeper hills. For example, 8% grade (about that of maximum on Tejon pass) would result in roughly 30 miles range at 25 MPH vs 25 miles range at 65 MPH. As a percentage, it's large, but 5 miles make little difference. If the destination is at the top of a hill, speed is largely irrelevant at grades more than 5%.
However, if one expects to drive beyond the hill top (going down or flat after climb), it may make sense to slow down a bit to save some energy.
Energy
But range isn't as useful. We don't typically drive uphill for entire battery capacity. What we'd like to know is how much energy is used to drive certain number of miles uphill. This would require 3D plot. Simpler is to take some boundary conditions: 25 MPH, 45 MPH, 65 MPH.
Following plots show the energy use over distance for various speeds. Since we're talking about shorter distances, we don't have to play safe with power, and we consider full power case. Power greater than 100kW are shown as full battery energy (not recommended / possible). But remember what I wrote in caveat above: they could be way off with higher power.
25 MPH case
45 MPH case
65 MPH case
Note that SparkEV cannot drive 34% grade at more than 45 MPH. It's just as well; those roads are local, and one should not speed on them.
GVWR case
All of the above are with 150 lb driver, probably the best case. With more passengers and cargo, weight will be more. The maximum weight is the gross vehicle weight rating. I can't seem to find this number through google, but I find it printed on the car's door as 3761 lb (3761-2866 = 895 lb of "cargo"). Only 2015 data is available.
But there is a problem. With added weight, there will be more friction from rolling from the tires and wheel bearings. Since the range polynomial was derived using "light weight" as cargo, it could be very different with full GVWR. Unfortunately, we can't do much about that since we don't have the data; we can only assume things will be worse. Did I mention I make stuff up?
Then we have the following. Remember, actual will be worse, though not quantified how much worse. And again, remember the caveat about higher power efficiency being much different than typical.
Something to note is that top speed at GVWR is only 40 MPH on 34% grade hills. It's just as well; on such steep hill, even 25 MPH might seem scary.
Recall from total power discussion above that I drove 55 MPH through 6% grade and the power display showed between 28 kW and 33 kW with two dogs, about 125 lb extra. Even if I had almost 750 lb extra, the power would be only slightly more, maybe around 35 kW. Of course, this still neglects the rolling resistance effect, but it should be pretty close.
Can SparkEV climb Tejon Pass?
In theory, SparkEV can easily climb over Tejon Pass. It's only 6% grade for about 12 miles.
First, let's check the power. 8% grade at 65 MPH is about 50kW (half power) while 5% grade is much less. 6% grade at 65 MPH would probably (PROBABLY) have similar efficiency as typical, so we can use above plots.
On the way down, it would recapture 50% to 75% of the energy via regenerative braking. But the problem is how much energy would it have when it gets to the bottom of the hill before the actual climb. If there's DCFC at the bottom of the hill, this is not a problem. Alas, that isn't the case.
Going from South to North as of Mar. 2016, closest DCFC is at Castaic (1200 ft), some 36 miles away from Gorman peak at about 4200 ft, difference of 3000 ft (0.57 miles).
23901 Creekside Rd, Santa Clarita, CA 91355
That is average of 0.57 / 36 = 1.6% grade. Let's assume 2% (red color plot from 65 MPH energy graph) and things operate within the model parameters (efficiency stays at typical levels).
2015 SparkEV would easily make it at 65 MPH for 35 miles of 2% grade with solo driver by using 70% to 80% of new battery capacity. Given that battery warranty kicks in at 65%, one could theoretically make it over the hill even with slightly worn battery. Remember, we need some margin, so we don't consider 100% case. Another interesting data is that average power required is roughly that of driving at 80 MPH on flat road.
For GVWR case, it's unknown, because the range polynomial doesn't take added rolling resistance into account. But we can guesstimate by taking 3% grade case (about double actual grade, cyan color plot). That shows 65 MPH for 35 miles to use over 90% of new battery capacity. Unless one has a new battery and charged to 100%, SparkEV isn't likely to make it over the hill. It's also about average power at 90 MPH on flat road.
But what if we go really slowly? It's too dangerous to drive at 25 MPH on freeway, so one should not do this. But as a thought experiment, is it possible? From 25 MPH graph, we see that 3% grade for 35 miles will need about 70% to 80% battery. So in theory, one can make it over the hill going really slowly. It's also about average power at 50 MPH on flat road, but going half the speed.
Going up to the top of the hill is one thing, but getting to the charger on the other side is equally important. Next DCFC is located at Selma, CA, some 180 miles away from previous DCFC at Castaic.
2950 Pea Soup Anderson Blvd, Selma, CA 93662
This would make it impossible to use DCFC to travel over Tejon Pass. There really need to be DCFC at the bottom of the hill on both sides for this to work. For now, the only option for SparkEV is along 101 freeway to travel between SoCal and NoCal as in my fictional trans CA EV race blog post.
http://sparkev.blogspot.com/2016/02/the-great-trans-california-ev-race.html
Theory
Theory on the basics of range polynomial was discussed in previous blog post, aptly named "range polynomial". Here, we add additional, which is basic Trigonometry and Physics.
 |
| http://i.stack.imgur.com/06flR.gif |
Percent grade on a hill is rise over run. Then the angle is simply the arc tangent of percent (divided by 100). A quick review of Trigonometric magic word, so-caaaa-toe-ahhhh.
SOH : Sine of an angle is Opposite side length divided by Hypotenuse length of a right triangle.
CAH : Cosine of an angle is Adjacent side length divided by Hypotenuse length of a right triangle.
TOA : Tangent of an angle is Opposite side length divided by Adjacent side length of a right triangle.
Quick side note: sine in Spanish is "seno" which is also the body part. Math and anatomy, like peas in a pod!
We invoke the TOA clause from above, and take inverse tangent (aka, arc tangent) to get the angle.
Angle = arctan (grade_in_percent / 100)
Once we have the angle, we can simply multiply the weight by the sine of the angle to find the additional force needed. Of course, we don't really need that at all; we can use Pythagorean theorem to bypass sine and tangent altogether, but that's left as exercise to your high school kids taking Trigonometry.
Once the force is known, we need to find the power needed to overcome the added force as the car is traveling up. Obviously, faster speed, quicker one would acquire potential energy. It's simply force multiplied by speed.
power_climbing = force * speed
Because the power is specified as kiloWatts, conversions are needed. Doing bunch of hocus pocus conversions from magic miles and pound and slugs to MKS units, we arrive at power just for the climbing portion in kiloWatts.
Because the operations are linear, power will simply add. You can prove it yourself or pay your kids to do it. We add flat road power from range polynomial to the additional power for climbing to get the total power for climbing at various speeds.
power_total = power_flat_road + power_climbing
Once we have the total power, we can multiply by time needed to travel some distance to find the required energy. Time, of course, is distance divided by speed. Once again, make sure the units are converted to MKS and arrive at the following.
Energy = power_total * time = power_total * (distance / speed)
After all this, we generate various plots of interest. Are they correct? It's homework!
Edit Apr. 5, 2016
After some discussion on unrelated topic of SparkEV's fake noise maker (thanks for poking me, Norton), aka Pedestrian Friendly Alert Feature, PFAF (completely useless as my Prius is silent), I thought of a new way to estimate rolling resistance. It is roughly when low speed has about 1/2 of the range of flat road. From above, that occurs at about 2% grade (65 miles at 10 MPH). That shows the force to be about 60 lb.
While air resistance may not be substantial at 10 MPH, static power of 1 kW could be taking significant portion. Plugging in the number to polynomial, 10 MPH result in 1.66kW, taking 60%. Then the rolling resistance force is 40% of 60 lb, or 24 lb.
One can experiment this value on flat road. Using a bathroom scale pressed against the back of the bumper, push the car until it's moving at constant speed. I read about 35 lb when I do this, though it's changing much due to irregular pushing. I think that's close enough, so it's about 35/3100 = 1.13%
Then the force calculation in appendix should change as follows. Since baseline includes the weight of the car and 150 lb driver, added force is only applicable to added weight minus the baseline.
if (year==2014) mass_baseline = (2967+150); end
if (year==2015) mass_baseline = (2866+150); end
force1 = ( mass_lb * sin(angle_radians) ...
+ ( mass_lb - mass_baseline) * 0.0113 * cos(angle_radians) ...
) / 2.2 * gravity; % Newtons
Below are new graphs for GVWR case for 2015. Range penalty is about 5 miles for low slopes with GVWR.
Appendix
As before, Octave is used to analyze and generate the plots. New convention is adopted for this m-file: those ending with "1" are vectors (1D arrays) and "2" are matrices (2D arrays). For example, "force1" would indicate 1D array of force values.
Copy-paste this into Octave to generate the plots or save to a file and play with it as you see fit. What grade would SparkEV fail to climb at any speed? What road would SparkEV fail to travel at specified speed limit due to steep grade?
clear; close all;
batt_2014 = 19;
speed1_2014=[0 24 55 62];
power1_2014=[1 3.33 10.2 12.7];
batt_2015 = 18;
speed1_2015=[0 30 55 60];
power1_2015=[1 3.9 10.6 12.73];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% power polynomial and max range
poly1_2014=polyfit(speed1_2014, power1_2014, 3)
poly1_2015=polyfit(speed1_2015, power1_2015, 3)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% range over slope
function added_power_vs_speed(year, mass_lb, poly1, batt)
speed1=0:5:90;
grade1=[0 1 2 3 5 8 13 21 34]; %grade in percent
mph2kmps = 0.44704 / 1000;
gravity = 9.8; %m/sec/sec
angle_radians=atan(grade1/100); %radians
% OLD! force1 = mass_lb / 2.2 * gravity * sin(angle_radians); % Newtons
if (year==2014) mass_baseline = (2967+150); end
if (year==2015) mass_baseline = (2866+150); end
force1 = ( mass_lb * sin(angle_radians) ...
+ ( mass_lb - mass_baseline) * 0.0113 * cos(angle_radians) ...
) / 2.2 * gravity; % Newtons
force2 = repmat(force1, length(speed1), 1)';
speed2 = repmat(speed1, length(force1), 1);
power_grade2 = force2 .* speed2 * mph2kmps; % kW extra for grades
figure; plot(speed1, power_grade2, 'o-'); grid on;
axis([min(speed1) max(speed1) 0 100]);
set(gca, 'xtick', speed1, 'ytick', 0:10:100);
xlabel('speed (mph)'); ylabel('power (kw)');
legend(cellstr(num2str(grade1')), "location", "northwest");
title ([num2str(year) ' extra power vs speed various % grades']);
% total power including extra power for grades
power1 = polyval(poly1, speed1);
power2 = repmat(power1, length(force1), 1) + power_grade2;
figure; plot(speed1, power2, 'o-'); grid on;
axis([min(speed1) max(speed1) 0 100]);
set(gca, 'xtick', speed1, 'ytick', 0:10:100);
xlabel('speed (mph)'); ylabel('power (kw)');
legend(cellstr(num2str(grade1')), "location", "northwest");
title ([num2str(year) ' total power vs speed various % grades']);
% ranges at slopes
range2 = speed2 * batt ./ power2;
range2(power2>50) = 0;
figure; plot(speed1, range2, 'o-'); grid on;
axis([min(speed1) max(speed1) 0 100]);
set(gca, 'xtick', speed1, 'ytick', 0:10:100);
xlabel('speed (mph)'); ylabel('range (miles)');
legend(cellstr(num2str(grade1')), "location", "northwest");
title ([num2str(year) ' range vs speed various % grades']);
%energy use over distance
miles2meters = 1/1609.344;
hour2seconds = 3600;
distance1 = 0:5:50;
for speed_a1 = 25:20:65
force2 = repmat(force1, length(distance1), 1)';
power_grade2 = force2 * speed_a1 * mph2kmps; % kW extra for grades
power2 = polyval(poly1, speed_a1) + power_grade2;
distance2 = repmat(distance1, length(force1), 1); %miles
time2 = distance2 ./ speed_a1; %hours
energy2 = power2 .* time2;
energy2(power2 > 100)=batt;
figure; plot(distance1, energy2, 'o-'); grid on;
axis([min(distance1) max(distance1) 0 batt]);
set(gca, 'xtick', distance1, 'ytick', round((0:(batt/10):batt)*10)/10);
xlabel('distance (miles)'); ylabel('energy (kWh)');
legend(cellstr(num2str(grade1')), "location", "northwest");
title ([num2str(year) ' energy vs distance at ' ...
num2str(speed_a1) 'mph various % grades']);
end
endfunction
added_power_vs_speed(2014, 2967+150, poly1_2014, batt_2014);
added_power_vs_speed(2015, 2866+150, poly1_2015, batt_2015);
added_power_vs_speed(2015, 3761, poly1_2015, batt_2015); %GVWR, 900 lb of cargo
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%resize all plots for easy viewing
% for n=1:18; a=figure(n); set(a, 'Position',[200,100,440,300]); end